新型コロナウイルス(SARS-Cov-2)による感染症が拡大してきて、
「いったいどこまで行くの?」っと頭を抱える方も多いでしょう。
わたしは収束が予想がつかなくてすごい恐怖を感じています。
よくニュースで、
「指数関数的に感染者が増加しています」っと聞きますが、
正直、指数関数というものがよくわからない人結構いるのではないでしょうか?
なので、指数関数的増加の説明とその恐ろしさを見ていきましょう!!
指数関数的増加とは
簡単に指数関数とは
「指数」というのは聞いたことあるでしょうか?
4の2乗は16とかいうところの、”2”の部分、
つまりaのn乗のnのことです。
んで、指数関数というのはすご~く簡潔に言うと
「y=a^x(aのx乗)であらわせるグラフのこと」
です。
つまり、a=2のとき
- x=1のときy=2
- x=2のときy=4
- x=3のときy=8
- x=4のときy=16
- x=pのときy=p^2
ということで、グラフにするとこう!

指数関数の特徴
ここでは、y=aのx乗(ただしaは1以上)を考えます。
x=1からx=2になるとき、yは2だけ大きくなっていますが、
x=3からx=4になるとき、yは8だけ大きくなっています。
xの値がどんどん大きくなればなるほど、xが1増加したときのyの増加する量はとてつもなく大きくなってくのがこの指数関数の特徴です。
(つまり坂がどんどん急になってるグラフの形)
このグラフの接線を考えるとより明確にその特徴が分かります。
グラフ上の接線の傾きの大きさというのは、その接点でのyの変化の大きさを表しています。(数学Ⅱ)
そして、y=a^xの接線の傾きというのは、微分することで、
接線の傾き=loge(a)×a^x (詳しいことは数学Ⅲでやってね☆)
この式からxの値が大きくなればなるほど、接線の傾きはどんどん急になって、
xが1だけ増えたときの傾きの変化もだんだん大きくなる。
つまり、xの値が増えれば増えるほど、xの増加分に対するyの増加量がどんどん大きくなるということです。
↑↑これ、覚えといてください!
指数関数的増加をまとめると
指数関数的増加とは、xが大きくなればなるほど、xが1上がったときのyが大きくなる量がおおきくなって、
やがて、そのyの増加量は信じられない位になる。
というのが指数関数的増加を簡単に説明したものです。
新型コロナウイルス感染者の増加
ここからは、新型コロナウイルス感染者の増加グラフをさっきの説明を踏まえて見ていきましょう!
日本国内の感染者数のグラフを例に見ていきましょう!
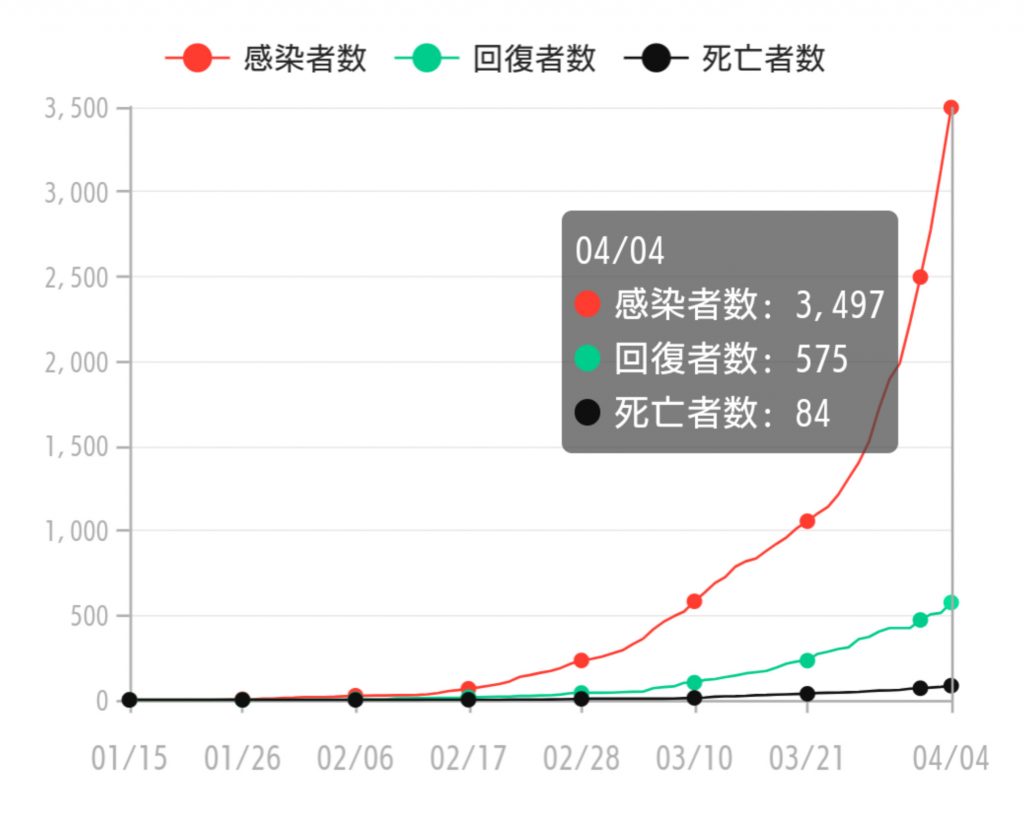
このグラフが日本の感染者数を表したグラフです。
日付をx軸、感染者数をy軸として、最初のほうのグラフと比較すると、
形が似ているということに気づくはずです。
つまり、指数関数的に増加していて、日がたてばたつほど1日の感染確認者がどんどん大きくなっているっということがわかります。
この指数関数的増加は4月4日までの見方であって、今後必ずしも指数関数的に増加するとは限りません。
指数関数的増加の恐ろしさ
今の日本のグラフを見て、この増加の仕方の恐ろしさを感じた人もいると思います。
もし仮に…そうはなってほしくないけど、もしも指数関数的増加を続けたら、
1日当たりの感染者数はとんでもないことになってしまいます。
4月4日で350人程度、3日と比べて50人増加…
このままどんどん1日の感染者が増加していけば、総感染者はとんでもないことになります。
恐怖を無理にあおりそうな記事になってしまいましたが、決してそんな気持ちで書いたわけではありません。
コロナを正しく知って正しく恐れてほしいのです。
この記事を読んだあなたがコロナを正しく恐れて、罹患しないことを願ってます。
こぼねごと
わたしなりの勝手な予想をします。
明確な根拠がない単なるわたしの考え(素人)なので、興味ある人はじっくり、ない人は戯言だと思って聞き流してください。
まず日本はしばらく指数関数的増加をつづけると予想します。
北海道は、基本再生産数を1を下回っていることから道外からの流入を防げば収束する可能性はある。
現在、欧州での増加は指数関数的増加でなくなっていることから、日本もある時期を境に基本再生産数が1を下回り収束へ向かう。
これが、わたしの頭の中です。
説得力は全くないことはわかっているのですが、一応書いときました。
コロナを正しく知って正しく恐れる。これほんっと大事です。
恐れすぎても心理的負担がすごいし、恐れなさ過ぎても罹患する。
「適当」ってだいじですね!
っということで今回もありがとうございました(*- -)(*_ _)ペコリ




コメント